Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 9 класс

На данной странице размещены олимпиадные задания с решением для 9 класса.
Олимпиада по математике прошла с 15 сентября по 2 октября 2022 года

Посмотреть ответы на все задания олимпиады

Посмотреть ответы на задания

Вопрос №	1	2	3	4	5	6	7	8	9	10	11	12	13
Ответ	В	Б	В	Б	72576	Б	Г	9980	Г	Г	700	Г	Б

Задача №1
На сколько нолей заканчивается факториал числа 500?
(A) 100
(Б) 120
(В) 124
(Г) 132
(Д) 140

Задача №2
В песне 20000 группы Nautilus Pompilius есть такие слова:
«Двадцать тысяч дней и ночей пройдёт,
Человек родился — человек умрёт.»
Предположим, что некоторый человек, для которого справедливы слова этой песни родился 1 января 2001 года. Прожив, включая день рождения эти 20000 дней он на 20001 день умирает. Найдите дату смерти человека из песни.
(A) 4 октября 2055 года
(Б) 5 октября 2055 года
(В) 17 октября 2055 года
(Г) 18 октября 2055 года
(Д) Ни одна из дат не верна

Задача №3
Дан куб размера NxNxN склеенный из N3 единичных кубиков (их сторона равна 1). Его поверхность покрашена в некоторый цвет. При каком значении N впервые количество кубиков хотя бы с одной окрашенной стороной станет меньше общего количества кубиков которые вообще не имеют ни одной окрашенной стороны?
(A) При N=8
(Б) При N=9
(В) При N=10
(Г) При N=11
(Д) При N=12

Задача №4
В прямоугольнике ABCD единичной площади отмечены точки L, M, N и P разбивающие стороны прямоугольника пополам и ещё , а точка O— середина отрезка NP. Найдите площадь треугольника OLM
Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 9 класс
(A) 5/16
(Б) 1/4
(В) 1/5
(Г) 1/6
(Д) 3/8

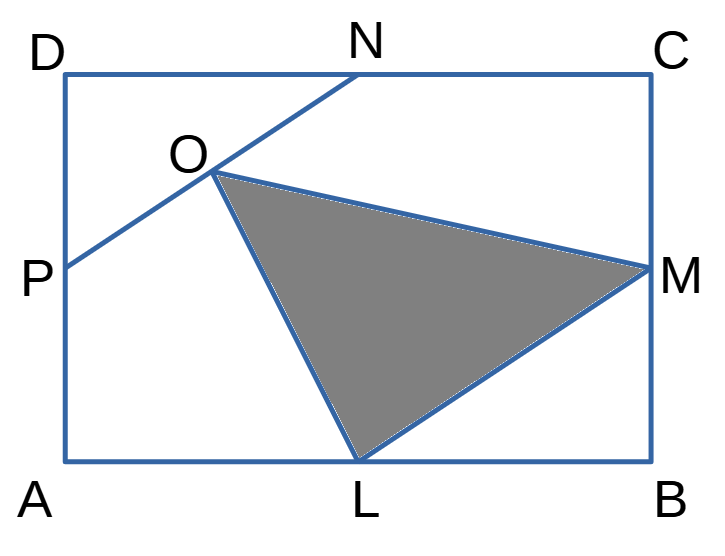
Задача №5
Сколько сотен секунд в дюжине недель (Введите свой ответ)

Задача №6
Пусть p и q — натуральные числа. Рассмотрим пять чисел: pq + 2, р2 + q3, (р + 1)(q + 1), (р + q)2, р(q + 1). Какое наибольшее количество чётных чисел может оказаться в этой пятерке?
(A) 5
(Б) 4
(В) 3
(Г) 2
(Д) 1

Задача №7
Во время сушки в сублимационном аппарате влага может удаляться со скоростью до 7 грамм/сек. В камеру загрузили 7 кг помидор с содержанием влаги в 93% и 4 кг перца с содержанием влаги 65% овощи нужно высушить до влажности 10%. Сколько времени это займёт минимум?
(A) 4 мин 30 сек
(Б) 4 мин 40 сек
(В) 4 мин 50 сек
(Г) 5 мин 0 сек
(Д) 5 мин 10 сек

Задача №8
Число назовем забавным, если оно 13-значное и нет никакого другого 13-значного числа с такой же суммой цифр больше него. Найдите 3 по величине (т. е. в порядке убывания) забавное число делящееся на 5 и введите его 4 младших разряда как одно число.

Задача №9
Значение выражения
Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 9 класс
равно:
(A) 2024
(Б) 2023
(В) 2022
(Г) 1012
(Д) 1011

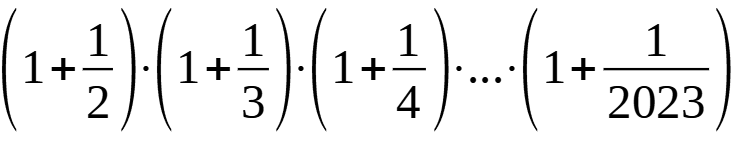
Задача №10
Какое множество точек задается на плоскости уравнением
Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 9 класс
А Б В Г Д
(А) А
(Б) Б
(В) В
(Г) Г
(Д) Д

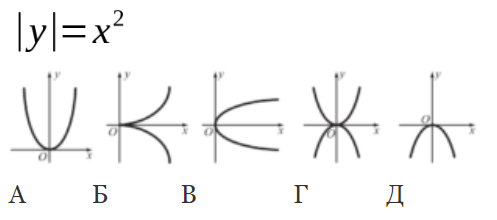
Задача №11
Фигура Циклоп может съесть свою жертву или переместиться в новую позицию если может добраться до неё двигаясь только по 2 направлениям из четырёх по границам сетки (можно, например, совершать сколь угодно много шагов вправо и вверх, но нельзя при этом делать ни одного шага влево или вниз)
Подсчитайте количество различных маршрутов для Циклопа (находящегося в т. А) позволяющих добраться до цели(в т. Б).
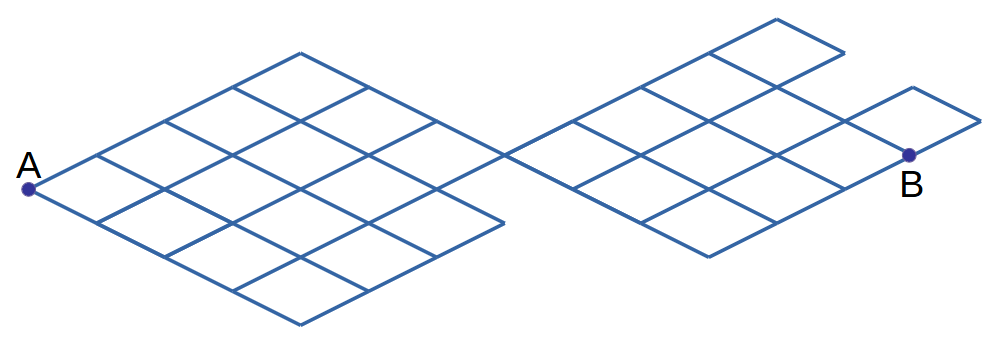
Задания Одиннадцатой Олимпиады по математике Осень 2022 1 тур 9 класс

Задача №12
Выполнение работ по проекту было оценено в 882 тыс. рублей на заработную плату из расчёта, что его будут выполнять (с условно одинаковой производительностью) 15 человек в течении 12 дней.
К работе приступили 8 человек и проработали 7 дней. После этого к бригаде добавили 3 человек и в этом составе они проработали 6 дней. Для скорейшего завершения проекта к бригаде на 4 дня добавили ещё 6 человек. После окончания основных работ проект был показан заказчику и на устранении недостатков работало 5 людей в течении 4 дней (остальные работники были распределены на другие проекты). Дальше работа была принята и выплачена оговоренная сумма.
На сколько меньше запланированного получит каждый работник в пересчёте на 1 день если всю полученную сумму разделили между всеми работниками пропорционально отработанным дням?
(A) На 240 рублей меньше
(Б) На 350 рублей меньше
(В) На 500 рублей меньше
(Г) На 700 рублей меньше
(Д) На 900 рублей меньше

Задача №13
Джон никогда не говорит правды. В один прекрасный день Джон в разговоре с Кристианом воскликнул : «По крайней мере один из нас никогда не лжет» Тогда будет справедливо утверждение:
(A) Кристиан всегда лжет
(Б) Случается, что Кристиан лжет
(В) Кристиан полностью правдив
(Г) Иногда Кристиан говорит правду
(Д) Джон не мог бы такое сказать