Задания Двенадцатой Олимпиады по математике Зима 2023 2 тур 9 класс

Задача №1.

Автор: Иванова Юлия

В команде программистов 40 человек. Из них на С++ пишут 20 человек, на Java — 15 человек, на Python — 11 человек. 7 программистов знают C++ и Java, 5 знают C++ и Python, и 3 человек — Python и Java. Один человек владеет всеми тремя языками. Все остальные занимаются frontend-разработкой и используют другие языки.
1) Сколько человек занимаются frontend-разработкой?
2) Сколько человек знает только один из языков C++,Python или Java?

Задача №2.

Автор: Бродский Давид

Докажите, что найдутся такие взаимно простые в совокупности натуральные числа a, b, c, d и e, большие , что

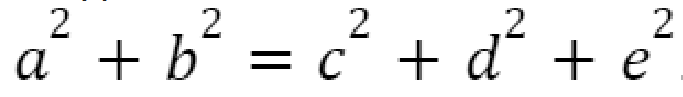
Задача №3.

Автор: Альперин

Найдите все тройки простых чисел p,q,r, удовлетворяющие системе уравнений:

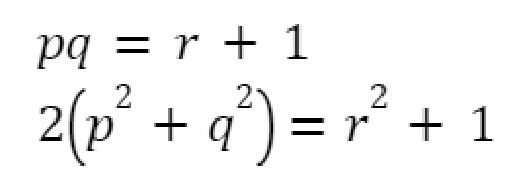
Задача №4.

Автор: Галиулина Варвара

Есть карточки с числами 754, 28, 78240, 103, 5271, 384 (с каждым числом может быть сколько угодно карточек). Можно ли разложить их по кругу так, чтобы у каждой пары чисел, стоящих рядом, была одинаковая цифра, и любая пара чисел с одинаковой цифрой встречалась рядом, но ни одна такая пара не попадалась дважды?

Задача №5

Автор: Иванова Юлия

Доктор Стрэндж защищает n миров Мультивселенной от темных сил. Чтобы проверить всё ли в порядке, он должен провести как минимум n минут в каждом из миров.  Из—за различий в размерностях миров время в них течет иначе: в k—ом мире время идет в k^2 раз медленнее (для всех k от 1 до n).
Например, пока Стрэндж проведет положенные n минут в (n-1)-ом мире, на Земле пройдет n(n-1)^2 минут.
Докажите, что среднее земное время проверки одного мира больше

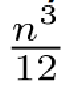
Задача №6.

Автор: Иванова Юлия

Докажите, что

при всех натуральных n.

Задача №7.

Автор: Иванюк Дмитрий

Золушке добрая мачеха подарила набор «Целочисленная геометрия», в котором есть большое количество палочек с длиной, равной целому числу сантиметров. Сегодня Золушка должна сконструировать все различные треугольники, используя палочки длиной больше 10 см, но не длиннее 20 см. Мачеха сказала, что, когда Золушка выполнит задание, она может поиграть на компьютере. Если каждый треугольник она составляет за 1 минуту и начала это делать в 18:00, то успеет ли она поиграть, а если успеет, то сколько, при условии, что спать она должна лечь в 22:00? Треугольники, совпадающие при вращении или  переворачивании, считаются одинаковыми. Ошибок и повторов золушка не допускает.

Задача №8.

Автор: Иванюк Дмитрий

В некоторой компании из 2N человек у каждого есть ровно три друга. Всегда ли её можно разбить на N пар друзей?