Задания 1-го тура XVIII олимпиады по математике для 9 класса
1 тур XVIII олимпиады по математике прошел с 16 по 29 июня 2025 г.
Задачи олимпиады
Задача №1
Двое мудрецов загадали по числу от 1 до 100. Сначала первый мудрец сказал: “Если твоё число делится на моё, то я буду знать, чему равно твоё число”. На что второй мудрец сказал: “Твоё число точно делится на моё”. Чему равно произведение загаданных мудрецами чисел, если их сумма равна 100?
А) Нельзя однозначно определить Б) 99 В) 900 Г) 1875
Галиулина В.Н.
Задача №2

Галиулина В.Н.
Задача №3
В банке 25 конфет пяти разных цветов, при этом конфет каждого цвета поровну. Какова вероятность, что взяв 5 конфет из банки мы возьмем конфеты не всех цветов?
А) 24/625 Б) 10001/10626 В) 625/10626 Г) 601/625
Булавинов Б.А.
Задача №4
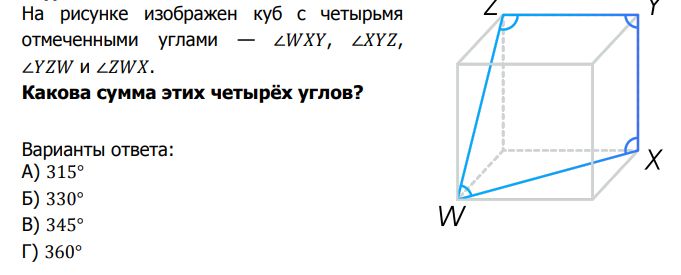
Галиулина В.Н.
Задача №5
Сколько решений в натуральных числах имеет уравнение 8a=3ab−12b?
А) 0 Б) 1 В) 2 Г) 3 Д) бесконечно много
Галиулина В.Н.
Задача №6
Отношение двух положительных чисел равно отношению их суммы к их разности. Каково это отношение?

Миронов Д.Р.
Задача №7
Половина окружности вписана в четвёртую часть в другой окружности как показано на рисунке. Каково соотношение площади половины окружности (меньшей части) к четверти окружности (большей части)?
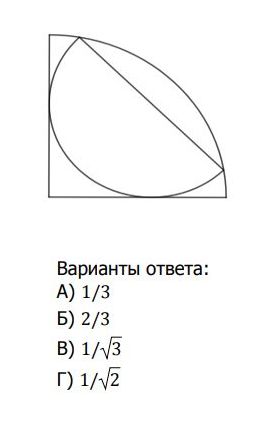
Миронов Д.Р.
Задача №8
Рассмотрим всевозможные прямоугольники с периметром 32. Чему равна минимально возможная длина диагонали в них?

Тодоров Е.И.
Задача №9
Петя выписывает на доску числа. Первые три числа — это 2, 3 и 5. Каждое следующее число равно сумме всех предыдущих минус их количество. Например, на четвёртом месте будет стоять (2 + 3 + 5) − 3 = 7, на пятом – (2 + 3 + 5 + 7) − 4 = 13 и так далее. Чему равна сумма членов этой последовательности с чётными номерами, не превосходящими 20 (то есть сумма второго, четвёртого, шестого, … и двадцатого членов последовательности)?
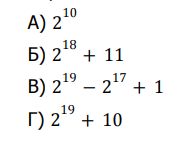
Тодоров Е.И, Галиулина В.Н.
Задача №10
В лавке с мороженым в летний день собралась очередь из 30 человек, и они начали обсуждать любимые вкусы мороженого. Назовём вкусы двоих людей схожими, если в списках их любых вкусов есть хотя бы один общий. Оказалось, что если взять любых двух человек (для удобства обозначим их X и Y) из очереди, то в очереди найдётся ещё хотя бы двое, вкусы которых будут схожи с X и Y. Назовём сладкоежкой человека, вкусы которого схожи со вкусами наибольшего количества людей в лавке (возможно, сладкоежек несколько). Какое наименьшее количество любимых вкусов может быть в списке сладкоежки?
А) 7 Б) 8 В) 9 Г) 10
| Задача № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ответ | Б | Б | Б | Б | В | Г | Б | Б | Г | В |
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно


