Задания 2-го тура XVIII олимпиады по математике для 7 класса
2 тур XVIII олимпиады по математике прошел 20 июля 2025 г.
Задачи олимпиады
Задача №1
Решите уравнение в целых числах:
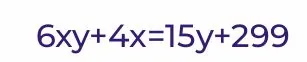
Задача №2
У математика есть двухчашечные весы и набор из 98 гирь: {1/3 кг, 1/4 кг, 1/5 кг,…, 1/100 кг}. Каким наименьшим количеством гирь набора с помощью чашечных весов можно уравновесить груз весом 1 кг?
Задача №3
Петя написал на доске выражение:
Вася хочет заменить звёздочки цифрами из набора 1, 2, …, 9, взяв каждую цифру не более одного раза, так, чтобы получить верное равенство. Сколькими способами Вася может это сделать?
Вася хочет заменить звёздочки цифрами из набора 1, 2, …, 9, взяв каждую цифру не более одного раза, так, чтобы получить верное равенство. Сколькими способами Вася может это сделать?

Задача №4
Все жители острова из племени Соглашателей или Отрицателей:
● Соглашатель говорит правдивое предложение, если предыдущее правдиво, и говорит ложное во всех прочих случаях.
● Отрицатель говорит правдивое, если предыдущее ложно, и говорит ложное во всех прочих случаях.
Однажды на острове собрались 10 человек. Каждый из них (в некотором порядке) по одному разу подошел к другому и упрекнул его в том, что этот человек (которого упрекнули) из племени Соглашателей. В конце все получили по одному упрёку.
Какое максимальное число людей из племени Отрицателей могло при этом быть?
● Соглашатель говорит правдивое предложение, если предыдущее правдиво, и говорит ложное во всех прочих случаях.
● Отрицатель говорит правдивое, если предыдущее ложно, и говорит ложное во всех прочих случаях.
Однажды на острове собрались 10 человек. Каждый из них (в некотором порядке) по одному разу подошел к другому и упрекнул его в том, что этот человек (которого упрекнули) из племени Соглашателей. В конце все получили по одному упрёку.
Какое максимальное число людей из племени Отрицателей могло при этом быть?
Задача №5
По кругу лежит 2025 монет орлом вверх. За ход можно указать на некоторые группы подряд лежащих 7 монет (в том числе можно пересекающиеся, но нельзя несколько раз одну и ту же) и эти группы перевернуть. Если какая-то монета в нескольких группах, то ее перевернут несколько раз. Можно ли за 2 разных хода (то есть множества групп, на которые указывали, не было одинаковым) вернуться в исходное положение (все орлы)?
Задача №6
Какое наименьшее количество ферзей можно поставить на доску 10*10 так, чтобы каждая клетка, которую ферзь не бьёт, была соседом по стороне клетки, которую ферзь бьёт?
Задача №7
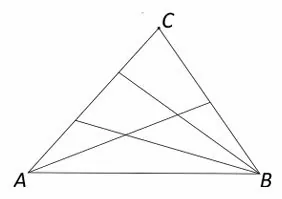
Вася провёл в треугольнике ABC отрезки из вершин A и B к противоположным сторонам треугольника (хотя бы один отрезок к каждой стороне, пример на рисунке) и посчитал сколько всего треугольников можно насчитать на его рисунке (стороны должны идти по проведенным линиям). Петя сделал то же самое, но количество отрезков у него могло быть другим. В итоге Вася насчитал на своём рисунке на один треугольник больше, чем Петя на своём. Обязательно ли кто-то из них ошибся?
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



