Задания V олимпиады по математике для 6 класса

В слове ЗЕЛЕНОГРАД каждая буква обозначает ненулевую цифру. Одинаковые буквы — одинаковые цифры. Разные буквы — разные цифры. Произведение всех цифр делится на 729. Чему равна сумма этих цифр?

Разделите фигуру на 4 равные части, чтобы в каждой части оказалась и звезда, и сердечко.

Конфеты в коробке лежат в виде прямоугольника. Если съесть все конфеты вдоль всех стенок, то останется столько же конфет, сколько лежит вдоль одной из стенок. Какого размера может быть коробка? Объясните, почему других вариантов нет.

Натуральное число N в три раза больше своего наибольшего делителя, отличного от него. Может ли это число быть в 10 раз больше какого-то другого своего делителя? Если такое число есть, то приведите пример. Если такого числа нет, объяснить, почему.

Можно ли квадрат разделить на выпуклые пятиугольники?

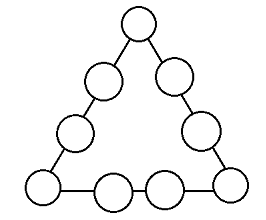
Ника вставила в пустые кружки числа от 1 до 9 так, чтобы на каждой стороне треугольника сумма была одинаковая. Чему может быть равна эта сумма? Найдите все варианты и объясните почему других вариантов нет.