Задания 2-го тура XVIII олимпиады по математике для 6 класса
2 тур XVIII олимпиады по математике прошел 20 июля 2025 г.
Задачи олимпиады
Задача №1
Все жители острова из племени Соглашателей или Отрицателей:
● Соглашатель говорит правдивое предложение, если предыдущее правдиво, и говорит ложное во всех прочих случаях.
● Отрицатель говорит правдивое, если предыдущее ложно, и говорит ложное во всех прочих случаях.
Однажды на острове собрались 10 человек. Каждый из них (в некотором порядке) по одному разу подошел к другому и упрекнул его в том, что этот человек (которого упрекнули) из племени Соглашателей. В конце все получили по одному упрёку.
Какое максимальное число людей из племени Отрицателей могло при этом быть?
● Соглашатель говорит правдивое предложение, если предыдущее правдиво, и говорит ложное во всех прочих случаях.
● Отрицатель говорит правдивое, если предыдущее ложно, и говорит ложное во всех прочих случаях.
Однажды на острове собрались 10 человек. Каждый из них (в некотором порядке) по одному разу подошел к другому и упрекнул его в том, что этот человек (которого упрекнули) из племени Соглашателей. В конце все получили по одному упрёку.
Какое максимальное число людей из племени Отрицателей могло при этом быть?
Задача №2
Дан белый квадрат 5×5. В нем можно закрашивать в черный любые 2 клетки, если они касаются друг друга углами или сторонами. После нескольких таких закрашиваний оказалось, что в любой строчке нет 2 соседних белых клеток. Какое максимальное число клеток могло остаться белыми?
Задача №3
Могут ли пять человек сыграть в бильярд за одним столом так, чтобы:
● каждый сыграл с каждым ровно по одной партии;
● никто не играл две партии подряд;
● никто не пропускал больше двух партий подряд?
● каждый сыграл с каждым ровно по одной партии;
● никто не играл две партии подряд;
● никто не пропускал больше двух партий подряд?
Задача №4
У старика Макдональда была ферма, на которой жили три лошади и три коровы. Однажды Макдональд решил построить для каждой лошади и каждой коровы по собственному загону, обнесённому забором. Для каждой лошади он хочет построить по треугольному загону с тремя сторонами по 9 метров, а для каждой коровы — по квадратному загону со сторонами по 6 метров. Каждый загон должен быть окружён забором со всех сторон, но если загоны ставить рядом, то между ними можно построить один общий забор, сэкономив дерево. Попробуйте расположить загоны так, чтобы сумма длин всех заборов вокруг них была наименьшей. Чему равна эта сумма?
Задача №5
У математика есть большие двухчашечные весы и набор из n гирь массой 1 кг, 2 кг, 3 кг, …, n кг. Известно, что он может ровно 2025 способами положить одну гирю на левую чашу весов и две на правую так, чтобы установилось равновесие. Сколько всего гирь может быть у математика?
Задача №6
Вася провёл в треугольнике ABC отрезки из вершин A и B к противоположным сторонам треугольника (хотя бы один отрезок к каждой стороне, пример на рисунке) и посчитал сколько всего треугольников можно насчитать на его рисунке (стороны должны идти по проведенным линиям). Петя сделал то же самое, но количество отрезков у него могло быть другим. В итоге Вася насчитал на своём рисунке на один треугольник больше, чем Петя на своём. Обязательно ли кто-то из них ошибся?
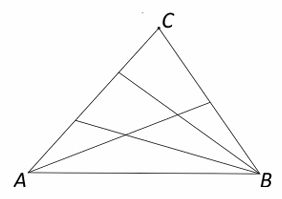
Задача №7
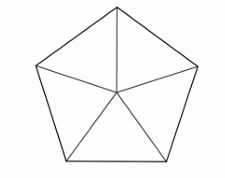
Максим нарисовал фигуру, и заметил, что её не получится нарисовать одним росчерком, то есть не отрывая карандаша от бумаги и проводя каждую линию только по одному разу. Какое минимальное количество линий нужно добавить к рисунку Максима, чтобы новую фигуру можно было нарисовать одним росчерком, не проводя ни по какой по линии дважды? Покажите пример такой фигуры и расскажите, как нарисовать её одним росчерком.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



