Задания 2-го тура XVIII олимпиады по математике для 8 класса
2 тур XVIII олимпиады по математике прошел 20 июля 2025 г.
Задачи олимпиады
Задача №1
Гарри Поттер купил в Лавке Олливандера волшебную “вечную” свечу. Первоначальная высота свечи - 30 см. Гарри заметил, что первый сантиметр свечи сгорел ровно за 15 минут, а каждый следующий сантиметр горит столько же, сколько все предыдущие вместе взятые. На сколько часов хватит свечи на самом деле?

Задача №2
Решите уравнение в целых числах:
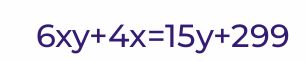
Задача №3
Петя написал на доске выражение: ** ∙ ** ∙ ** = 2025 Вася хочет заменить звёздочки цифрами из набора 1, 2, …, 9, взяв каждую цифру не более одного раза, так, чтобы получить верное равенство. Сколькими способами Вася может это сделать?
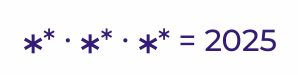
Задача №4
В стране Числонии есть города с названиями от 1 до 20. Сначала из каждого города с меньшим номером провели авиалинию в каждый город с большим номером. Будем называть заменой авиалинии ситуацию, когда из авиалинии ведущей из A в B делают авиалинию, ведущую из B в A. Сначала заменили одну авиалинию из 2 в 20 город. А затем несколько раз брали какой-то город и заменяли все авиалинии, которые ведут из или в него. Докажите, что в любой момент будут такие три города A, B и C, что из A есть линия в B, из B есть линия в C и из C есть линия в A.
Задача №5
Есть клетчатый квадрат 6×6, в котором некоторые клетки черные, а остальные белые. Известно, что в любом клетчатом прямоугольнике внутри, у которого обе стороны больше 1, хотя бы один из угловых квадратиков белый. Сколько максимум черных квадратиков?
Задача №6
Чемпионат по футболу с участием 16 команд проходил в один круг (каждая команда играла с каждой ровно один матч; за победу дается 3 очка, а за ничью 1 очко). В очередном туре все команды разбиваются на пары и команды из каждой пары проводят матч между собой. При каком наименьшем k могло оказаться, что после k туров уже определена команда, которая получит 1-ое место и команда, которая получит 2-ое место, и результаты следующих матчей не могут на это повлиять?
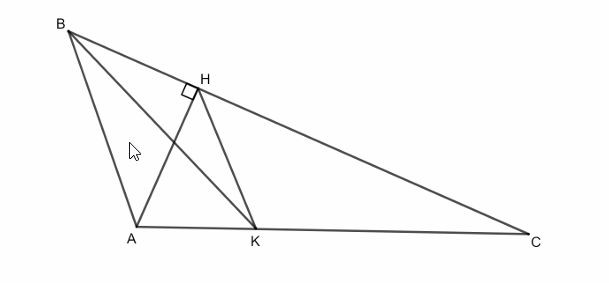
Задача №7
AH – высота треугольника ABC (Н лежит на стороне BC). На стороне AC нашлась точка K такая, что BK=KC и AH=HK. Докажите, что прямая HK делит площадь треугольника ABC пополам.
I тур: 15 сентября - 27 сентября 2026
II тур: 25 октября 2026
Олимпиада по математике
Двадцать первая международная
Участвуйте в очередной математической олимпиаде от Систематики! Олимпиада проходит в два тура, по итогам которых победители получают ценные призы грамоты и дипломы.
Регистрация участника
Бесплатно



